频谱泄露与窗函数
在FFT(傅里叶变换)分析信号时,常常会提到频谱泄露现象,即某频率谱线的幅值分布到其他频段。这样会严重影响信号频率和幅度的判断,为了减轻这种现象,使用窗函数进行截取,即加窗。
一,频谱泄露现象
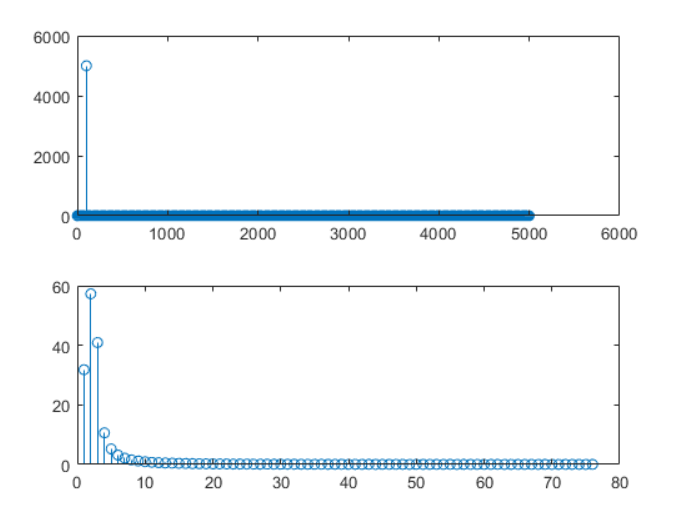
对原信号做非周期截断后进行FFT,得到的频率谱线会出现旁瓣,即出现原信号频率之外的的频谱,同时原信号幅度降低,可视为原信号的能量泄露到附近频点上。
非周期截断:
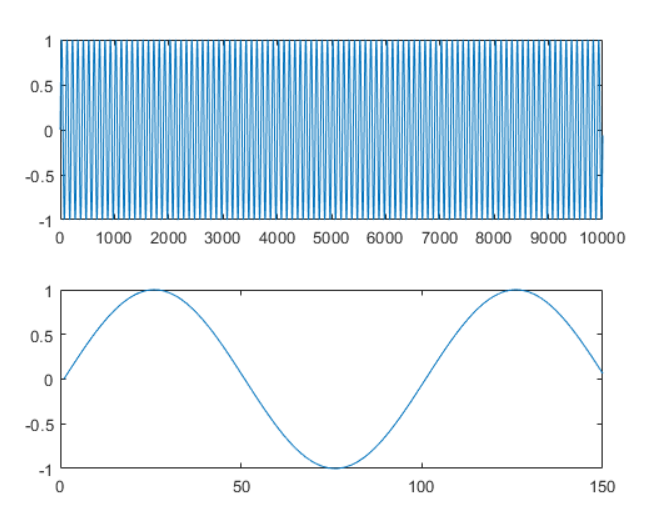
做FFT后有频谱泄露:
二,周期截断与非周期截断
信号截断
由于实际信号处理时,我们不可能将整个原始信号进行FFT,只能截取信号的一部分进行处理,这个过程就叫信号截断。
根据截取信号的长度与周期的关系,可以分为周期截断和非周期截断。
周期截断
如果截取信号的长度为原信号周期的整数倍,则截断后的信号依然为周期信号,可以重构为原始信号,进行FFT后的频谱频率成分为原信号频率,100%幅度。
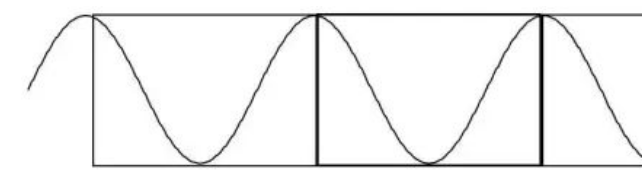
假设原始信号的频率为f Hz,则周期为1/f s,截取信号的时间长度为T=k/f。则频率分辨率为1/T=f/k。那么原信号频率成分为f=k*1/T,即有一条谱线正好是原信号频率成分。
非周期截断
如果截取信号的长度不是原信号周期的整数倍,则截断后的信号不是周期信号,重构出来的信号不连续,出现跳跃。
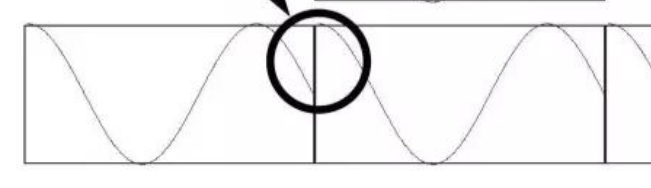
对这种信号进行FFT后,频谱会分散,原信号频率成分的幅值不再是100%。反而原信号周围谱线出现幅值,即泄露到了周围频谱。
非周期截断中,没有一条谱线与原信号完全相同。
三,FFT变换
根据傅里叶变换的推导,我们可以知道周期信号可以用傅里叶级数表示,即使用频谱中的一些离散点表示。而对非周期信号,只能用连续的频谱去无限逼近,因此非周期截断会出现泄露。
四,窗函数
引入窗函数前,先来直观理解一下什么是窗。我们对信号进行截断,就好像在信号上面套了一个窗户,我们只能看见窗户里面的信号,用这里面的信号去分析原信号。这就是加窗的直观理解。
为什么要使用窗函数
窗函数就是给窗内信号的每个点都加上一个权值,使窗内信号的起始和截止幅度都为0,让窗里面的信号变成周期信号,从而减少频谱泄露(不能消除)。
常见窗函数
各种窗函数频谱特征的主要差别在于:主瓣宽度(也称为有效噪声带宽,ENBW)、幅值失真度、最高旁瓣高度和旁瓣衰减速率等参数。不同的窗函数具有不同的频谱特征。
- 主瓣宽度主要影响信号能量分布和频率分辨能力。频率的实际分辨能力为有效噪声带宽乘以频率分辨率,因此,主瓣越宽,有效噪声带宽越宽,在频率分辨率相同的情况下,频率的分辨能力越差。
- 旁瓣高低及其衰减率影响能量泄漏程度(频谱拖尾效应)。旁瓣越高,说明能量泄漏越严重,衰减越慢,频谱拖尾越严重。
矩形窗
如果直接对信号截断,则窗内的信号权重都为1,这种窗称为矩形窗。
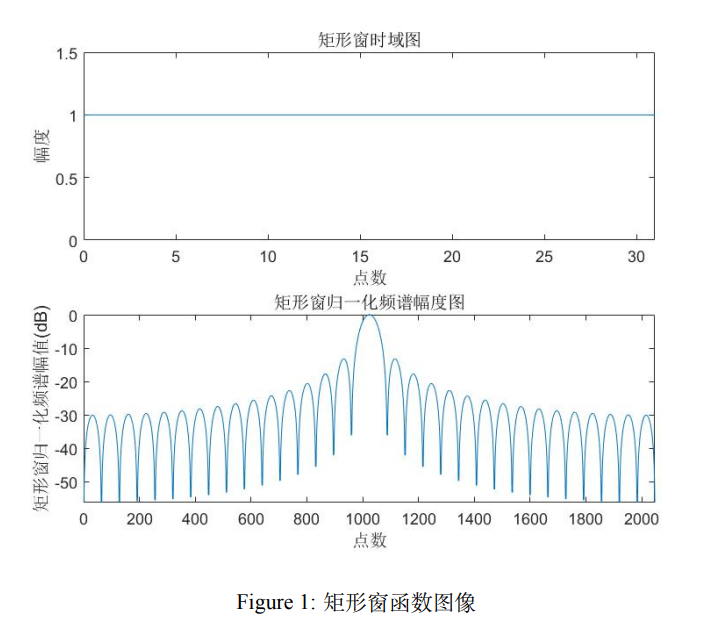
这种窗的优点是主瓣比较集中,缺点是旁瓣较高,而且可能伴有负旁瓣,频谱泄漏 现象会较为严重. 特点就是可以保证测量时的频率较为精确,但是不能保证幅值测量的精确性.
三角窗
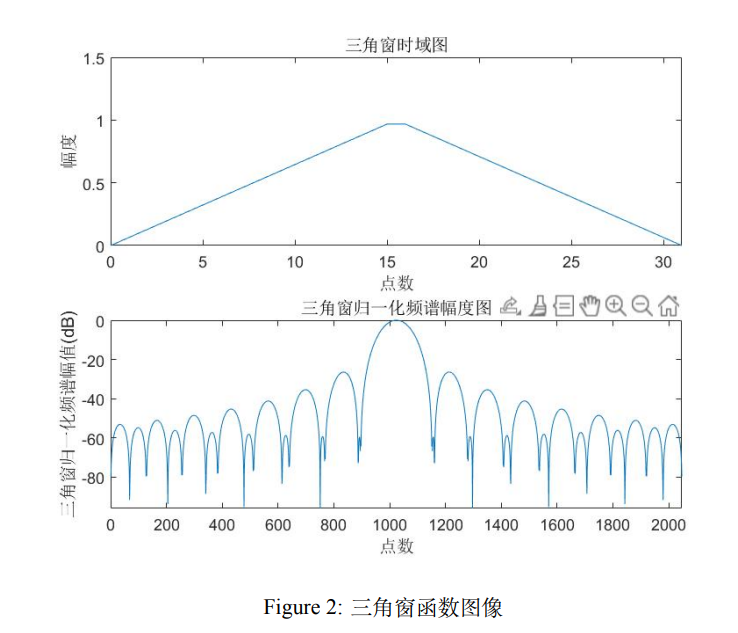
三角窗使用渐进的权重,让边界处的信号为0,这种窗其主瓣宽度比矩形窗宽约一倍,旁瓣 相比于矩形窗非常小,测幅度会准一些但测频率就差。
汉宁窗
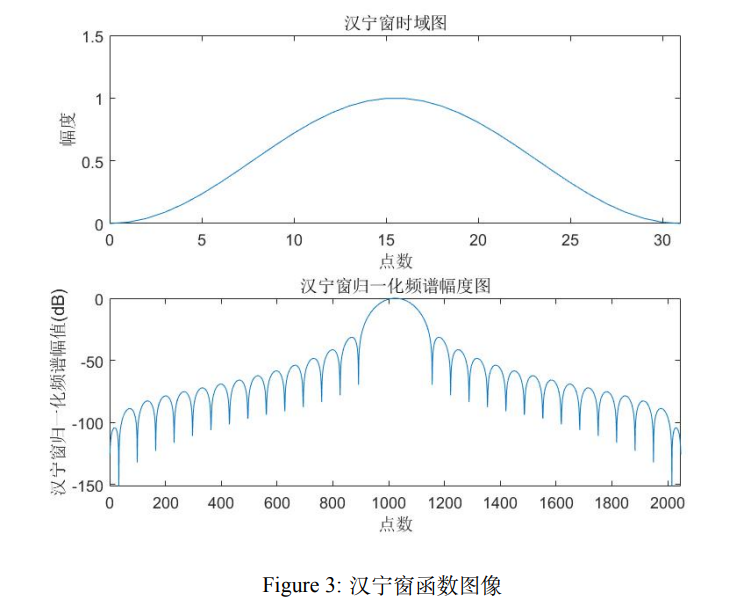
汉宁窗会增加主瓣宽度,导致频率分辨率下降。
汉明窗
汉明窗和汉宁窗基本一致,不一致的只有一个参数。
凯泽窗
其中 N 为序列的长度,I0 的零阶的第一类修正贝塞尔函数,α 是任意非负实数,用于调整凯 泽窗的外形,由使用者根据实际情况给定。
平顶窗
常见窗函数参数
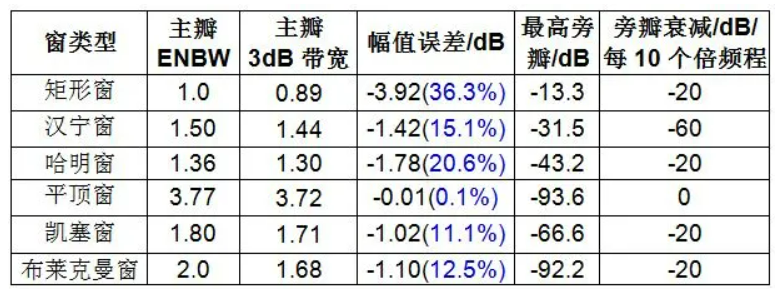
根据此表可以估计窗函数性能,帮助选择。
窗函数选择
加窗函数时,应使窗函数频谱的主瓣宽度应尽量窄,以获得高的频率分辨能力;旁瓣衰减应尽量大,以减少频谱拖尾,但通常都不能同时满足这两个要求。因此需要根据实际需求选择合适窗函数。
这里给出一个参考:
- 如果截断的信号仍为周期信号,则不存在泄漏,无须加窗,相当于加矩形窗。
- 如果信号是随机信号或者未知信号,或者有多个频率分量,测试关注的是频率点而非能量大小,建议选择汉宁窗。
- 对于校准目的,则要求幅值精确,平顶窗是个不错的选择。
- 如果同时要求幅值精度和频率精度,可选择凯塞窗。
- 如果检测两个频率相近、幅值不同的信号,建议用布莱克曼窗。
- 锤击法试验力信号加力窗,响应可加指数窗。