对带通采样定理的理解

奈奎斯特采样定理要求采样频率必须大于信号频率的2倍，不然会发生频谱混叠。但是对于高频信号，ADC难以达到所需要的采样率。实际上，我们进行频谱分析时，只需要让我们需要信号的频率不发生频谱混叠就行了，由此就出现了带通采样定理。

一，奈奎斯特采样定理和带通采样定理

奈奎斯特采样定理又称低通采样定理。其“低通”的含义是从0频率到信号中角频率最大的分量都能复原，不发生频谱混叠。这样就要求以0为中心2*w宽度的频段都必须没有重叠：

这就是所谓低通。

但这样会导致两个中心频率相距至少要2*w以上，即采样频率为原信号的两倍，对采样率要求极为苛刻。

很多时候，我们的关注的信号频率主要集中于高频段，对低频信号不关心。如图，我们只关心高频很窄的一段信号：

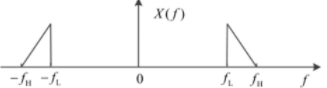
这就是所谓带通。

理解什么是带通后，我们对其进行分析。

对于奈奎斯特采样定理，我们要求采样频率在我们关心的频率范围内（0-最大频率分量）不发生频谱叠加。因此对于带通采样，我们同样只要求在我们需要的频率内不发生频谱叠加。

随着采样率的增加，采样信号频谱周期延拓的周期越来越大，在这个过程中，我们只需要取带通的频谱不重叠的采样频率就行了。

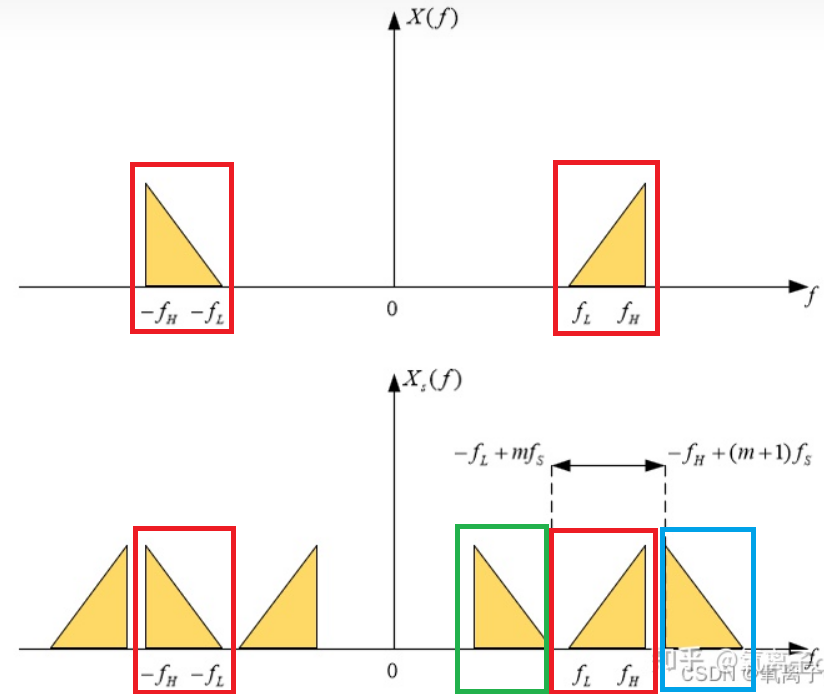
（偷一下氧离子大佬的图）

红色的是原信号，绿色和蓝色是采样导致的周期延拓出来的信号。

可以看到，我们只需要保证绿色和蓝色的频谱不和红色的频谱重合，就不会发生频谱重叠，我们依然可以得到想要的信号。

将上面的要求用数学公式表达出来：

那么就可以得出采样频率的要求是：

显然，存在条件是：
$方框代表向下整，为整数$
可见，当m=0，就是奈奎斯特采样定理。

假设一个信号的频率在45-55MHz的范围，那么对采样率的要求是

那么可以得到：

最小采样率被降低到了原来的二分之一左右。