对Nyquist-Shannon采样定理的直观理解

奈奎斯特(香农)采样定理是信号采样中需要遵守的重要定理，即采样频率至少为信号频率的两倍，才能还原原信号。这里给出对其原理的直观理解。

一，时域与频域的联系

在讨论具体的采样定理前，首先需要一点基础。

在信号与系统中我们学到，对一个冲激信号，其在频域上是1。

而对于1，频域上是一个冲激。

如果将1视为周期无限小的冲激信号，但冲激信号的周期从无限小到无限大时，频域上的最开始周期无限大的周期信号也逐渐变成周期无限小的周期信号，最终变成1。

那么从这个过程我们可以得到直观的结论：

• 时域连续，频域离散，反之亦然。
• 采样后的信号频谱是原始信号频谱的周期延拓，延拓周期就是采样角频率。

对于第二个结论，这里有着科学的证明：采样定理推导(The Nyquist–Shannon sampling theorem)（本文章的图也来自于这里）

二，采样定理

知道采样信号的频谱是原信号的周期延拓后，我们就可以直接理解采样定理了。

如果一个信号的频谱为下图这样：

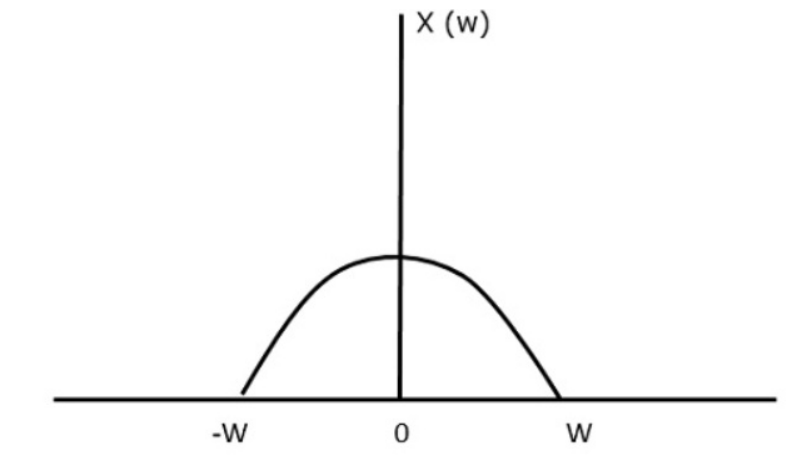
图中的w是该信号中频率最大的信号分量，这个区间内的信号就原信号的全部频谱。

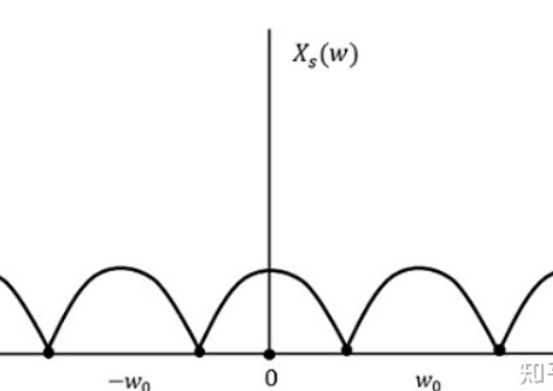
那么对该信号进行采样后，频谱就会变成该信号的周期延拓:

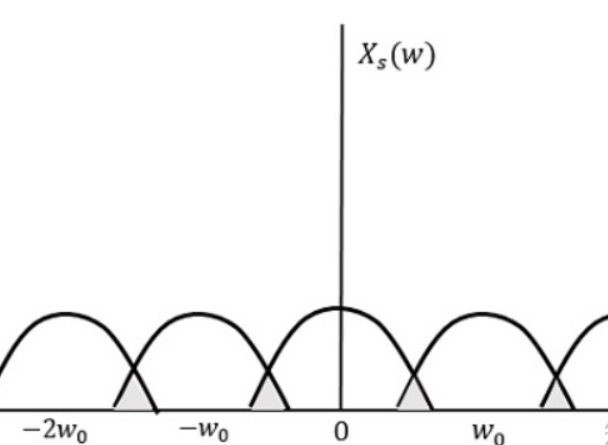
Wo就是采样的角频率，在上图情况中，采样频率小于信号频率的两倍，导致频谱间相互叠加，原信号无法复原。

当采样频率大于信号频率的两倍时，频谱就不会叠加了。这时可以得到原来的信号。